El poeta y físico argentino Claudio Archubi (Mar del Plata, Argentina, 1971) piensa lo bello0 y lo sublime, según lo entiende Kant, desde las matemáticas y la física. Archubi es Doctor en Física e investigador de CONICET. Actualmente trabaja en el IAFE (Instituto de Astronomía y Física del Espacio) y es docente de la Universidad de Buenos Aires. Colabora con revistas literarias del país y del exterior. Ha participado en varios festivales internacionales de poesía. Mención única dehonor en el concurso de poesía de la editorial Ruinas Circulares 2012 y menciones en cuento y poesía 2014. Segundo premio de poesía del Concurso de Letras 2019 del Fondo Nacional de las Artes; segundo premio en el Concurso Nacional de Poesía Victoria Ocampo 2021; finalista en el Premio de Poesía Ciudad de Salamanca 2021 y mención de honor en el Concurso de Poesía Vuelo de Quimera 2022. Su libro La casa sin sombra ha sido seleccionado, traducido al inglés y publicado en la antología bilingüe: África vs Latinoamérica. Escritura experimental (Langaa RPCIG, Camerún, 2017). Publicó La forma del agua (cuentos, ed. de la Universidad de La Plata, 2010), Siete maneras de decir tristeza (poemas en prosa, Lima, 2011), Sísifo en el Norte (poemas en prosa, ed. Ruinas Circulares, Buenos Aires, 2012), La casa sin sombra (poema en prosa, Buenos Aires, 2014), la ciudad vacía (ed. Trópico Sur, Uruguay, 2015), La Máquina de las alegorías (poemas en prosa, ed. Buenos Aires Poetry, Buenos Aires, 2016), Arca rota jardín de nadie (ed. Valparaíso, España, 2018) y Cielo al revés (Metafísica de la imagen de “Teresa” soñando el Sur) (ed. La primera vértebra, Buenos Aires, 2020).
En la montaña de Jano:
Sobre lo bello y lo sublime en Matemática, Física y Poesía.
Cuando era joven y todavía trepaba por los escabrosos filos del lenguaje científico, solía soñar con paisajes magníficos: castillos de agua, grandes olas o una montaña cuyas dos laderas eran como planos inclinados que servían de lecho a un gran lago. Había en ellos algo tremendo y fascinante, para citar a Rudolf Otto, quien recurre a estas cualidades para definir lo sagrado. Pero también había una belleza tranquilizadora donada por esas construcciones de la imaginación de alta simetría y simplicidad. En particular, recuerdo bien esa montaña caprichosa donde yo contemplaba, desde una ladera, el espejo celeste de un lago inclinado y cómo, a medida que el sol giraba para perderse en la ladera no visible, era acompañado por el desplazamiento lento del agua hacia esa ladera oculta como si fuera la otra cara de la luna.
El paisaje era inmenso, era bello, y era absurdo porque no respetaba las leyes básicas e intuitivas de la mecánica. Más allá de las connotaciones psicoanalíticas, recuerdo que al despertar me sonreí avergonzado y sorprendido por este prototipo dinámico tan absurdo como esos diagramas que violan la perspectiva en un dibujo de Escher.
Si creyera en la astrología, podría aventurar que era porque yo había nacido en enero. Bajo la marca del dios Jano, dios bifronte, de los principios y los finales. Y en el sueño quizá había tocado su arquetipo, una montaña de dos caras, la visible y la invisible, dos caras inseparables unidas por un mecanismo enigmático.
Pero no creo en la astrología y esa experiencia simbólica me parece relevante por motivos más cercanos al texto que nos proponemos transitar: ¿Qué cualidades de la imagen me produjeron la emoción de agrado e inquietud que la alimentó y la rescató del olvido incluso por encima de un montón de experiencias de la vida consciente?
En este texto buscaré un paralelismo entre la emoción estética en la poesía, en la matemática y en la física. Con ese fin voy a abordar panorámicamente una colección de casos. No pretenderé ser exhaustivo en esta casuística. Me interesa, antes que profundizar en los detalles técnicos específicos de cada ejemplo, hacer un rastreo breve que muestre la faceta ambivalente que adquiere la emoción estética en estas disciplinas y cómo interviene incluso como parámetro epistemológico.
Los pensadores más destacados han indagado sobre la belleza con miradas distintas desde el principio de la historia, desde Platón hasta Adorno. No obstante, para limitar el campo semántico, motivado por uno de los criterios de belleza relevantes a nuestro análisis, el de simplicidad y claridad, tomaré como punto de referencia la dupla intuitiva que plantea Kant en su libro “Observaciones acerca del sentimiento de lo bello y lo sublime”.
Kant retoma la idea original de lo sublime propuesta por el filósofo griego Dionisio Longino (s. III d.c.) y procesada luego por los místicos cristianos. Dos clases intuitivas de emoción estética propone Kant en ese humanizado y sencillo librito (1), tan distinto a su trilogía sistemática de la crítica de la razón. Vayamos a sus palabras:
Este delicado sentimiento que ahora vamos a considerar es principalmente de dos clases: el sentimiento de lo sublime y el de lo bello. La emoción es en ambos agradable, pero de muy diferente modo. La vista de una montaña cuyas nevadas cimas se alzan sobre las nubes, la descripción de una tempestad furiosa o la pintura del infierno por Milton, producen agrado, pero unido a terror; en cambio, la contemplación de campiñas floridas, valles con arroyos serpenteantes, cubiertos de rebaños pastando; la descripción del Elíseo o la pintura del cinturón del Venus en Homero, proporcionan también una sensación agradable, pero alegre y sonriente. Para que aquella impresión ocurra en nosotros con fuerza apropiada, debemos tener un sentimiento de lo sublime; para disfrutar bien la segunda, es preciso el sentimiento de lo bello. Altas encinas y sombrías soledades en el bosque sagrado, son sublimes; platabandas de flores, setos bajos y árboles recortados en figuras, son bellos.
“La noche es sublime, el día es bello (…)”
En párrafos posteriores, va más allá distinguiendo distintos tipos de emoción asociada a lo sublime:
Lo sublime presenta a su vez diferentes caracteres. A veces le acompaña cierto terror o también melancolía, en algunos casos meramente un asombro tranquilo, y en otros un sentimiento de belleza extendida sobre una disposición general sublime. A lo primero denomino lo sublime terrorífico, a lo segundo lo noble, y a lo último lo magnífico.
Y por último, detecta una cualidad que hace de frontera geométrica entre las dos clases principales de emoción: el tamaño.
Lo sublime ha de ser siempre grande; lo bello puede ser también pequeño.
Una montaña vista desde abajo es sublime terrorífica porque nos muestra nuestra propia pequeñez y nos confronta a la idea de la finitud y por consiguiente nos conduce a pensar en la muerte. Una montaña vista desde la cima es magnífica porque nos hace sentir seguros y poderosos y nos proporciona una sensación de expansividad del yo sobre su entorno.
La tragedia es angustiante y queda pegada a lo sublime terrorífico porque involucra la idea de la muerte y de la pequeñez del hombre frente al tiempo, que es infinito. Afirma Kant que, como contrapunto, la comedia produce en general un efecto relajante a través de la risa y por eso está más cerca de lo bello. Sin embargo, ambas implicarían una ruptura de la causalidad lógica. La primera, porque el infinito atenta contra la lógica deductiva. La segunda, porque una de las claves de la risa es el absurdo. Así que, a mi entender, por la comedia también entraría solapadamente la sensación de lo abismal.
El período clásico —con el acento puesto en la claridad, la simpleza, la simetría y la proporción (que no es más que un tipo específico de simetría asociado, a mi entender, al concepto aristotélico del arte como imitación de la naturaleza o mímesis)—, aquella época en que los dioses todavía estaban presentes, no sería sino un gran ejemplo de valoración de lo bello.
El romanticismo, surgido como reacción al iluminismo, dando valor a la oscuridad y al misterio, a la monstruosidad —falta de simetría y proporción—, y a la desmesura, perseguiría expresar lo sublime, tanto en su dimensión noble (persiguiendo la armonía, como se planteaba en una primera etapa del movimiento romántico), como en su dimensión terrorífica (como se planteó en una segunda etapa). Hay una faceta interesante que se hace muy marcada en este tipo de belleza: a diferencia del concepto de belleza clásica, donde hay pura presencia, en el romanticismo aparece la faceta de la conexión con la totalidad a través del misterio: un Dios que se hace presente porque sentimos su ausencia, esa dualidad entre revelación y ocultamiento. Esta idea de belleza romántica está marcada por el gnosticismo de Plotino (cuya influencia se hace muy marcada a partir del renacimiento, cuando frente a la inminente caída del imperio bizantino, se rescatan y se traducen al latín obras griegas hasta entonces desconocidas en Europa) y por el misticismo de los primeros padres de la iglesia, como San Agustín: Dios es un misterio que escapa a la razón; bondad (de la cual emana la belleza), unidad, verdad e inmensidad, se consideran atributos divinos. Los románticos proponían que el Yo es como un vaso capaz de contener la inmensidad de Dios, y expresarlo en el Arte mediante símbolos. El símbolo es un recurso poético pero también epistemológico. A diferencia del modelo científico, el símbolo alberga en sí mismo una dimensión carnal y un misterio, pues posee infinitas interpretaciones y así la posibilidad de contener a Dios. El misterio es superior a un enigma así como el símbolo tendría más alcance que la metáfora. El enigma es algo a descifrar lógicamente. El misterio es algo indescifrable. La ciencia apuesta a que la naturaleza es un enigma. La mística, a que es un misterio. Pero si la naturaleza fuera enteramente un misterio, no habría ciencia posible.
No obstante, esta mirada es simplificadora. Baste señalar que Novalis parte de una imagen extraída de los jardines de la belleza clásica: la flor azul. Y los dioses griegos cometían todo tipo de monstruosidades y desmesuras.
Lo bello y lo sublime en Poesía:
No es el propósito de esta exposición perderse en intentos de delimitar cuál es y hasta dónde llega el vasto territorio de la poesía sino observar cómo estas dos facetas de la emoción estética se manifiestan en dos ejemplos emblemáticos. Es obvio que existe una belleza formal muy presente en el poema tradicional, dada por los recursos sonoros como la métrica, el ritmo otorgado por la sintaxis y el corte de verso, la cesura y la rima, tomando como caso emblemático el soneto. Pero la belleza formal no lo es todo. Existen máquinas de rimar pero no de poetizar, afirmaba Octavio Paz. La música es un arma de doble filo en estos casos ya que sin una mirada reveladora puede transformar el texto en una máquina sin alma. Y es que el alma del poema es la mirada que nos ofrece del mundo. Esto lo ha comprendido la poesía contemporánea, que ha ido tomando distancia del modelo de la métrica y la rima para apuntar a una clase de texto donde se destaca la mirada sobre las cosas. Un ejemplo muy conocido es este poema de Williams Carlos Williams (1883-1963) (2):
Sólo para decirte
Que me he comido
las ciruelas
que había en
la heladera
Y que
probablemente
guardabas
para el desayuno
Perdóname
estaban deliciosas
tan dulces
y tan frías
Los recursos sonoros se reducen al ritmo que otorga el corte de verso, y los recursos poéticos también obedecen a una economía de elementos sorprendente. Aun así, se puede sentir la emoción estética. ¿Dónde está la belleza? El centro de gravedad se desplaza de la forma a la mirada. Este poema transmite la tranquilidad de una realidad cotidiana compartida por dos personas y las ciruelas se convierten en el símbolo afectivo del vínculo tácito entre ambos. Lo bello se manifiesta en la simpleza, la pequeñez y la ternura que se desprenden de esta nota, y en la humildad de una poesía que ha renunciado a toda altisonancia para valorar lo más contingente. Aunque siendo atrevidos y menos humildes como lectores, podríamos llevar la lectura mucho más allá de la intención del autor pensando esas ciruelas, que el poema torna tan valiosas, como la hostia ritual de esa relación. Está lejos, está oculto en lo circunstancial de un objeto cualquiera; pero cuando el poema lo enmarca, rodeándolo de una pureza nueva, por allí está asomando el infinito. En la época de escritura de este poema, a mediados del siglo XX, recurrir a esta simpleza fue original, pero también un modo personal del poeta para distanciarse de sus pares europeos y buscar una lengua propia: quien se enfrenta por primera vez a este tipo de poesía, se siente en presencia de una revelación porque es obligado a contemplar la realidad desnuda de todo ornamento, casi con la inocencia de un niño: oh sorpresa, las cosas son esto. Lamentablemente, duran los perezosos imitadores hasta el día de hoy en nuestro país y en otros tantos, perdiendo casi todo el mérito o el sentido revelador esta clase de poesía.
¿Significa que debemos volver a la métrica? La libertad formal nos permite prescindir de esa necesidad y emigrar hacia formas más variadas y complejas, —así como la geometría ha migrado de los sólidos platónicos a los “ya no geométricos” fractales—, formas que nos conducen, por ejemplo, de un tipo de belleza clásica a otro más barroco.
Veamos un ejemplo de un poema que apuesta a otro tipo de belleza (3):
45
El universo se investiga a sí mismo.
y la vida es la forma
que emplea el universo
para su investigación.
La flecha se da vuelta
y se clava en sí misma.
Y el hombre es la punta de la flecha.
El hombre se clava en el hombre,
pero el blanco de la flecha no es el hombre.
Un laberinto
sólo se encuentra
en otro laberinto
Económico en lo formal, este poema de Roberto Juarroz (1925-1995) apuesta a la emoción de vértigo que produce la complejidad del pensamiento. Remedando la silogística, está planteado en forma de premisas y una conclusión. La imagen central es la de un proceso cíclico: la flecha se da vuelta y se clava en sí misma. Es un esquema imposible similar a un dibujo de Escher. En lógica, este esquema se corresponde con la falacia del círculo vicioso o petición de principio. Y sin embargo, en física se corresponde con un comportamiento de la naturaleza: los denominados procesos de retroalimentación. Un ejemplo es el caso de la inducción electromagnética: el campo eléctrico que varía produce un campo magnético que al variar produce un campo eléctrico que produce un campo magnético y así hasta el infinito; es la ecuación de onda electromagnética. Entonces esta flecha, que nos remite a las paradojas de Zenón, ahora simboliza otro proceso que parece imposible pero existe: la retroalimentación. Un símbolo antiguo muy conocido vinculado a estos procesos y a la idea de ciclo es el símbolo alquímico de Uroboros, la serpiente que se muerde la cola: representa a la naturaleza como un ciclo infinito de creación y destrucción. La última imagen del poema nos recuerda a la de los espejos enfrentados, que representan una regresión al infinito. Entonces, esa flecha circular, provocando la sensación de paradoja e inmensidad en este poema, nos señala en la dirección de lo sublime. La obra de Juarroz, al romper las categorías de la lógica, provoca una suspensión del pensamiento, nos mueve el piso donde estamos apoyados y nos expande en el vacío con una sensación de vértigo e inquietud: Poesía vertical. Opera casi exclusivamente apelando a la inteligencia y llega al impacto emocional de esa manera.
Lo bello y lo sublime en Matemática:
Guillermo de Ockham, un pensador del siglo XIV, afirmó que no hay que multiplicar los entes sin necesidad. Es el principio conocido como «navaja de Ockham» o «principio de economía». Una hipótesis es tanto mejor cuanto más explica con menos elementos teóricos. La idea de Ockham, que apunta a ser un principio epistemológico, hereda implícitamente una de las características contenidas en el concepto de belleza clásica: la simplicidad. La simplicidad permite que la inteligencia abarque con menor esfuerzo al objeto y eso otorga una sensación de placer y tranquilidad, que se corresponde con lo bello tal como lo define Kant.
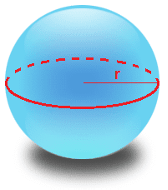
La simetría está asociada a la simplicidad: si doy vuelta un objeto o si lo veo en un espejo o si lo agrando o lo reduzco conservando sus proporciones, entonces digo que le he aplicado una transformación de simetría. Si el objeto no ha cambiado sus propiedades, entonces digo que es simétrico. Con menos parámetros se puede caracterizar ese objeto cuanto más simétrico sea. Por ejemplo, los sólidos platónicos. Para Platón, había cinco sólidos básicos con un alto grado de simetría y un sólido perfecto: la esfera. La esfera, donde todo punto se halla equidistante del centro, tiene un alto grado de simetría: es invariante frente a reflexiones y rotaciones. En el espacio cartesiano la superficie de la esfera está descripta por una sola ecuación. Y basta el radio para caracterizarla. Aunque un cubo aparezca ante nuestra intuición como algo tan simple, lo es menos que la esfera. En el espacio cartesiano, la superficie de un cubo requiere dieciocho ecuaciones, tres para determinar los puntos pertenecientes a la superficie de cada lado. Un cubo pierde simetrías de rotación y sólo conserva algunas para rotaciones específicas: 90, 180, 270 grados.
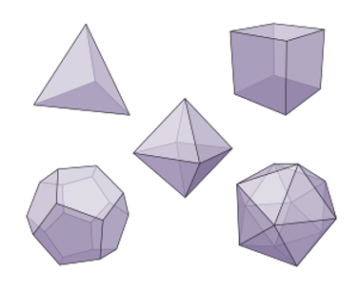
Sólidos platónicos
La ecuación de la esfera es: x2+y2+z2=r. r es el radio de la esfera. Ahora agregamos una variable más: x2+y2+z2+w2=r. Tenemos una hiperesfera en el espacio de cuatro dimensiones. Esto no es visualizable. Pasamos de lo bello visible a lo bello invisible. Sigue siendo formalmente bello bajo el criterio de simplicidad y simetría, pero no se puede visualizar. Así decimos que en matemática hay belleza formal, que puede ser visualizable a través de una representación espacial o no. Paralelamente observamos que como todo objeto geométrico parece tener su representación algebraica, se puede reducir la geometría al álgebra aplicando la navaja de Ockham.
Guiado por el principio de simpleza, el brillante filósofo inglés Bertrand Russell (1872-1970) se entusiasmó con la navaja de Ockham y en sus Principia Mathematica (1910) (4) quiso llegar a explicar toda la matemática como un sistema deductivo que obedece a las leyes lógicas bajo el formalismo de Frege (considerado uno de los padres de la lógica matemática, por su propuesta sistemática publicada en 1879, que sumaba al álgebra de Boole, la teoría de predicados). Ya unas décadas antes, había comenzado un proceso de formalización matemática de la lógica aristotélica (Boole, 1849) reduciéndola a un cálculo algebraico-proposicional y conduciendo poco a poco a la idea de que Lógica y Matemática debían ser sistemas formales equivalentes. Russell, por su parte trabajó en la reducción del concepto de número a la lógica de conjuntos y halló equivalencias entre la lógica de conjuntos y la de predicados, ampliando también esta última con aportes propios.
Russell tenía un espíritu clásico.
Russell quería un mundo claro, bello y ordenado por el amor y el conocimiento. Escribió libros sobre Filosofía, Matemática, Pedagogía, y hasta Ética. Era tan prolífico como nuestro compatriota muerto hace unos años, Mario Bunge. Ambos vivieron casi hasta los cien años. Como anécdota que rompe con los estereotipos, este caballero inglés se casó cuatro veces y era tan vital que a edad avanzada sufrió un naufragio y sobrevivió nadando hasta la costa. Sin embargo, esta victoria vital en su confrontación con lo sublime terrorífico no pudo lograrla con su propósito de fundamentar lógicamente la matemática.
En su intento de reducir la matemática a un sistema lógico-axiomático Russell enfrentó dos problemas graves: 1) La matemática no es completamente deductiva: el principio de inducción matemática (suponer que es válido para uno, luego para el siguiente, y concluir que es válido para todos), base del concepto de número y sus propiedades, no es un principio deductivo. 2) El teorema de Gödel: es imposible demostrar que toda proposición matemática es demostrable.
Hay una cita de Borges (5), que estaba al tanto de algunas de estas cuestiones paradojales, muy atinada al caso:
Hay un concepto que es el corruptor y el desatinador de los otros. No hablo del mal cuyo imperio limitado es la ética; hablo del infinito.
El infinito, responsable de la necesidad de introducir el principio inductivo, abre una fisura en el intento de simplificar la matemática siguiendo el criterio de belleza clásica de la economía para reducirla a la lógica deductiva. El infinito agujerea las redes del álgebra y la lógica y nos devuelve a lo abismal. Abre la puerta al sentimiento de lo sublime en Matemática. Y está escondido en la idea más básica de la matemática: el número.
Contar significa establecer una correspondencia uno a uno entre un conjunto de objetos (por ejemplo, los dedos de la mano) y otro cualquiera. Pero no terminamos de contar nunca un conjunto infinito. De acuerdo al intuicionismo matemático, el infinito no es algo dado, sino que siempre es una posibilidad, algo a lo que se tiende, algo, diríamos en términos aristotélicos, que siempre está en potencia, nunca en acto. Y la lógica deductiva trabaja con elementos que están completamente dados. El infinito escapa de sus redes. Siempre me han asombrado los números reales. Si comenzamos a contar los números reales que existen en un pequeño intervalo, digamos entre 0 y 1, no terminamos nunca. Son infinitos. Son tantos como el conjunto completo de los números enteros. Tal es el fundamento de las paradojas de Zenón. La flecha nunca se moverá porque para moverse tiene que recorrer un intervalo espacial, pero para llegar al final de este intervalo, debe llegar primero a la mitad, y antes, a la mitad de la mitad, y así infinitamente. Esta idea de la infinitud de un intervalo cualquiera, nos dice que en lo pequeño está escondida la inmensidad. Se abre la puerta de la emoción estética de lo sublime. Entre el cero y el uno, los dioses se ríen de nosotros.
Así como se construye la idea de número mediante un proceso iterativo infinito, también mediante un proceso iterativo infinito se puede construir gráficamente el concepto de fractal determinista. Un fractal tiene dos características relevantes: la dimensión y la invariancia de escala (homotecia=simetría de ampliación). Un ejemplo básico es el del fractal de Sierpinski. Este fractal se construye con triángulos, partiendo un triángulo en cuatro triángulos interiores (de esos cuatro, el triángulo central está invertido y se deja como hueco). Este fractal tiene dimensión 1.58 (menor que la dimensión 2 del plano porque queda espacio sin llenar). La principal característica de un fractal es la invariancia de escala. El patrón estructural se repite a toda escala. Es decir, si a cada uno de los tres triángulos llenos, los vuelvo a partir en cuatro, obtengo la misma estructura que se repite en los triángulos pequeños con un hueco central invertido más pequeño y así hasta el infinito.
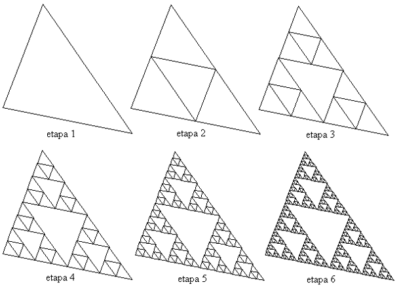
Fractal de Sierpinski
Y si la construcción del fractal involucra variables aleatorias (no determinista) vamos direccionando la matemática (que es el lenguaje de la física y tal vez, como diría Galileo, el de la naturaleza) de lo bello a lo sublime.


Fractal de rayos / Rajaduras en forma de fractal de hexágonos
Lo bello y lo sublime en Física:
Cuando empecé a estudiar física, nunca faltaban compañeros que se ilusionaban con la posibilidad de encontrar una teoría propia que explicara el universo. Y es que la inteligencia humana está motivada por el ideal clásico de belleza: la simpleza y la simetría. La mente humana experimenta placer cuando logra abarcar en una idea simple (como diría Descartes, en ideas claras y distintas), la realidad visible e invisible. Así, antes de profundizar nuestro conocimiento acerca de cualquier tema tendemos a una mirada demasiado simplificadora, somos como los niños: por eso en física decimos que cuando un modelo teórico omite muchos aspectos importantes del fenómeno físico a estudiar no es más que un modelo de juguete. Pero por algún lado hay que empezar.
Hay un ensayo de Borges (5), “La esfera de Pascal”, que va rastreando desde Parménides hasta Pascal, la idea de que el universo no es más que una esfera infinita cuyo centro está en todas partes y la circunferencia en ninguna. En este ensayo, Borges propone la tesis de que tal vez la historia humana no sea más que la historia de unas cuantas metáforas. Modificando esta idea y llevándola a la idea de modelo científico, un poco inspirados por Popper, podríamos proponer que tal vez la historia de la ciencia no sea otra cosa que una sucesión interminable de modelos de juguete cada vez más sofisticados, en busca de la biyección perfecta e inalcanzable entre la mente humana y la naturaleza misma. Dos ejemplos de esta sucesión histórica de modelos que van, cada uno de ellos, de lo más simple a lo más complejo, se ven en la escala de lo macro y de lo micro: el modelo astronómico y el modelo atómico.
Así, en función de cierta idea clásica de belleza formal, siempre al comienzo nos sentimos inclinados a aplicar la navaja de Ockham. Pero también, como en Poesía, en Física tenemos algo que en Matemática se presenta tan sólo en el ámbito gráfico: la belleza sensorial. Así como en un soneto tenemos belleza formal y belleza de contenido, el contenido de una teoría está asociado al fenómeno natural que intenta explicar. Una teoría puede ser bella con una belleza puramente formal y abstracta (la teoría de campos o el ejemplo de la hiperesfera en matemática), pero también la sensación de belleza de esa teoría puede expandirse por la belleza natural del fenómeno que intenta explicar, si este es impactante a los sentidos; por ejemplo, en lo visual, o en lo acústico.
Un ejemplo en la astronomía del goce de ambos tipos de belleza (formal y natural) nos lo da el filósofo Giordano Bruno (1548-1600), antes de que la física misma se constituyera como disciplina científica. Fue Giordano Bruno quien, aplicando el criterio de simplicidad, rompió con la dualidad aristotélica, sosteniendo la invariancia de las leyes físicas y la isotropía del universo: como es abajo es arriba y es igual hacia todas partes. Pero a la vez él sentía un profundo goce contemplativo al enfrentarse a la naturaleza porque la concebía en forma panteísta como manifestación divina. El universo es infinito porque dios lo es. Conocer la naturaleza era conocer a dios. Y conocer a dios nos convertía a nosotros mismos en dioses. El renacimiento nos dio a los últimos intelectuales optimistas que, a la vez que cuestionaban las ideas del cristianismo, platónicamente todavía creían que la mente humana podía acceder a un conocimiento absoluto de dios y del universo.
Para observar cómo los parámetros clásicos de belleza (simpleza y simetría) motivaron desde siempre la investigación científica, basta retroceder hasta estos modelos revolucionarios que marcaron el comienzo de la física como ciencia.
El modelo Ptolemaico (modelo geocéntrico platónico de órbitas circulares+epiciclos) (s.I-II d.c.) tenía que recurrir a una hipótesis adicional para explicar el movimiento de los planetas alrededor de la tierra: Los epiciclos. Órbitas circulares más pequeñas que harían los planetas alrededor de un punto abstracto de la órbita principal, similares al movimiento que veríamos que hace la luna alrededor de la Tierra si nos paráramos en el sol. Desde la Tierra se ve que algunos planetas parecen retroceder en sus órbitas circulares así como se vería retroceder la luna desde el sol. Se ve algo así como una trayectoria con rulos. Esto era espantoso a los ojos de Platón y por ello surgió la idea del epiciclo. Arreglar con otros círculos pequeños lo que las órbitas circulares no pueden explicar. Copérnico logró evitar gran parte de este problema cambiando el centro del sistema solar de la Tierra al sol.
Otro personaje importante guiado por un afán místico-estético fue Kepler (1571-1630). En su última gran obra “La armonía del mundo” (6), escribe:
Los movimientos celestes son tan sólo una inacabable canción para varias voces (percibidas por el intelecto, no por el oído); una música que, con discordantes tensiones, con síncopas y cadencias(…) avanza hacia un final ideado de antemano.
Kepler quiso ir más lejos y usar los sólidos platónicos para modelar las órbitas planetarias: en su modelo parte de una esfera exterior, que representa la órbita de Saturno dentro de la cual va inscribiendo sucesivamente: un cubo, la esfera de Júpiter, un tetraedro, la esfera de Marte, un dodecaedro, la esfera de la Tierra, un octaedro y finalmente la esfera de Mercurio. Pero al final tuvo que desecharlo, luego de comprobar que, de acuerdo a las observaciones astronómicas de Brahe, las órbitas eran consistentes con la figura de una elipse. Fue un caso fallido de aplicación del criterio de belleza clásica con fines epistemológicos.
- P. Crease, historiador de la ciencia, hizo que los lectores de la revista Physics World en el año 2002 votaran cuáles son los diez experimentos más bellos de la física.
Aquí se trata otra vez de la belleza en su sentido clásico: la simplicidad lógica del aparato y del análisis de sus resultados, que no son confusos ni ambiguos y aportan un resultado original y de impacto sobre el comportamiento de la naturaleza.
En la cima del ranking figura el experimento de la dualidad onda-partícula imaginado durante muchos años, desde el comienzo de la mecánica cuántica, como un experimento mental, y realizado finalmente por Jönsson en 1961. En este experimento de interferencia ondulatoria de un haz de electrones que atraviesa una doble ranura, catalogado como el más bello del mundo, más que en ninguno de los otros de la lista, el impacto estético se manifiesta de dos maneras: belleza formal clásica por la simplicidad del experimento y belleza paradojal del fenómeno que se estudia, por donde se cuela la sensación de vértigo propia de lo sublime. Cuando se quiebran los parámetros usuales donde la inteligencia está acostumbrada a pararse se produce asombro, pero también intranquilidad y vértigo porque sentimos que no tenemos asidero para el pensamiento: aparece lo abismal. Y unido a eso, lo sublime. El carácter dual del electrón como onda y partícula produce esa ruptura.
Por otro lado, a través de la moderna teoría de fractales, la física intenta encontrar orden y simetrías (belleza clásica) incluso en aquellos fenómenos que producen la sensación de lo sublime. El uso más sobrecogedor de la teoría de fractales, donde lo sublime (si como dice Kant, queda definido por la sensación de inmensidad) se hace totalmente presente, es para modelar la distribución de estrellas en el universo en galaxias, cúmulos de galaxias, super-cúmulos, etc.
Retrocediendo ahora hasta los comienzos de la física atómica, otro ejemplo interesante, donde detrás de lo bello se esconde lo sublime, ocurre cuando Marie y Pierre Curie descubren el radio. Estos físicos a finales del siglo XIX observaron que dentro de unas piedras que mandaron a traer de una mina de Europa y que emitían rayos que ellos utilizaban en experimentos haciéndolos impactar contra láminas muy delgadas, había otra sustancia que emitía, en forma más intensa y concentrada, rayos que al impactar contra el blanco producían una bella luz verde que persistía en la oscuridad.
Las piedras eran de uranio y la sustancia esa era el radio. Marie Curie murió de cáncer. El mismo fenómeno de radioluminiscencia fue aprovechado por una empresa norteamericana en la década de 1930, que empezó a pintar las manecillas y los números de los relojes, para que brillen en la oscuridad, con pintura que contenía radio. Las primeras en padecer los efectos mortales de la radiación fueron las empleadas de la empresa, a quienes se les recomendaba mojar el pincel con la lengua para una labor más eficiente. A partir de ese evento, se prohibió el uso del radio y el efecto luminiscente se logra en la actualidad mediante otras sustancias en dosis energéticas que no son dañinas.
Por último, los reactores nucleares también emiten una hermosa luz azulada. Lo que brilla no es la radiación en sí, nunca lo es (la radiación es invisible), sino que aquí los electrones de alta energía del agua, excitados por la radiación emiten ondas electromagnéticas a velocidades tan altas que se produce efecto doppler (radiación Cherenkov).
Esto muestra otra vez el carácter ambivalente de la belleza, ya que en estos casos, detrás de lo bello se esconde una idea terrible vinculada a lo sublime.
Vamos cerrando todo este artículo con una idea bastante actualizada por los últimos acontecimientos mundiales: el ángel de la Historia, imaginado por Walter Benjamin a partir del cuadro de Klee, ese que gira la cabeza para ver ruina tras ruina apilarse hasta el infinito ¿es el ángel de la entropía?
Pero no quiero dejar de subrayar que incluso en la idea del caos del devenir universal tan pegado a lo sublime terrorífico, hay momentos maravillosos que corresponden a lo bello: la vida humana misma puede entenderse como un sistema metaestable que es producto de estos procesos entrópicos. Volvemos entonces a la imagen del dios Jano, el dios bifronte de los comienzos y los finales. Porque todo este artículo tal vez no ha sido otra cosa que el torpe intento para explicar ese sueño de la montaña y el lago que se escurría al lado no visible, tan bello por su simetría y su simplicidad, pero tan ambivalente y paradójico: he construido mi modelo de juguete. Así como el electrón es una onda o una partícula dependiendo de la forma de observarlo, la belleza tiene este carácter dual tanto en el arte como en la ciencia. Detrás de lo bello se esconde lo sublime. Inmerso en lo sublime, nada lo bello.
Notas
- Observaciones sobre el sentimiento de lo bello y lo sublime, Immanuel Kant (Ediciones Libertador, Buenos Aires, 2004)
- Cien poemas, William Carlos Williams (Colección Visor de Poesía, Madrid 1988)
- Poesía vertical 1958/1982, Roberto Juarroz (Editorial EMECE, 1993)
- Principia Mathematica, Alfred Witehead and Bertrand Russell (1910)
- Obras completas, Jorge Luis Borges (Editorial Sudamericana, 2011)
- La armonía del mundo, Johannes Kepler (1619)





